문제 설명
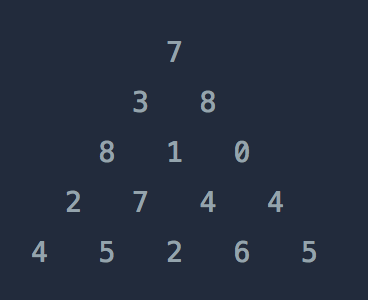
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
나의 풀이
DP 카테고리의 문제이기 때문에 당연히 DP 스타일로 풀어야 풀리겠다 생각은 했지만, 일단 DFS 방식으로 문제를 풀어봤다. 코드2 가 그 내용인데 숫자가 많은 케이스는 시간초과로 테스트 통과 실패. DP방식으로 다시 풀어봤다. DP의 가장 큰 특징은 이전에 계산한 내용을 저장이기 때문에 매 차수 계산한 값중에 큰값을 저장하는 방식으로 문제풀이를 접근했다.
문제 풀이의 핵심으로는 아래 3가지인데,
1. 삼각형안에서 각 행에 좌우 끝단은 받을 수 있는 숫자가 1가지 뿐이기 때문에 누적되는 값은 고정이 된다.
2. 좌우끝단이 아닌 자리의 수는 받을 수 있는 수가 2가지 이다. 때문에 매번 자기 위에 숫자 2가지 중 큰 수를 선택하고 주어졌던 값과 더 해준다.
3. 마지막 행에서 가장 큰 값이 전체 계산 값중에 가장 큰 값이다.
결과는 테스트 통과. 재귀함수를 통한 문제해결법만 반복하다가 DP를 처음 접했을 땐 참 헷갈렸는데, 공부를 하다보니 상당히 매력적인 방식이라 느껴진다.
코드1 (DP방식)
import java.util.*;
class Solution {
public int solution(int[][] triangle) {
int[][] arr = new int[triangle.length][triangle.length];
arr[0][0] = triangle[0][0];
for(int i=1; i<arr.length; i++) {
arr[i][0] = arr[i-1][0] + triangle[i][0];
arr[i][i] = arr[i-1][i-1] + triangle[i][i];
}
for(int i=2; i<arr.length; i++) {
for(int j=1; j<i; j++) {
arr[i][j] = Math.max(arr[i-1][j-1], arr[i-1][j]) + triangle[i][j];
}
}
int answer = 0;
for(int i=0; i<arr.length; i++) {
answer = Math.max(answer, arr[arr.length-1][i]);
}
return answer;
}
}
코드2 (DFS방식)
import java.util.*;
class Solution {
static int N;
static int Max = 0;
public int solution(int[][] triangle) {
int acc = 0;
N = triangle.length;
acc = triangle[0][0];
recur(1, 0, acc, triangle);
return Max;
}
static void recur(int depth, int begin, int acc, int[][] triangle) {
if(depth==N) {
Max = Math.max(Max, acc);
return;
}
for(int i=begin; i<=begin+1; i++) {
acc += triangle[depth][i];
recur(depth+1, i, acc, triangle);
acc -= triangle[depth][i];
}
}
}'Algorithm > Programmers-Algorithm' 카테고리의 다른 글
| Programmers 도둑질 java 풀이 (0) | 2020.09.01 |
|---|---|
| Programmers 등굣길 java 풀이 (0) | 2020.08.31 |
| Programmers 여행 경로 java 풀이 (0) | 2020.08.27 |
| Programmers 단어 변환 java 풀이 (0) | 2020.08.26 |
| Programmers N으로 표현 java 풀이 (0) | 2020.08.24 |